Bội số là gì? Bội số chung nhỏ nhất? Cách tìm bội chung nhỏ nhất là một phần kiến thức vô cùng quan trọng trong chương trình Đại số lớp 6. Cùng tìm hiểu chi tiết về bội số, bội số chung nhỏ nhất và áp dụng giải các bài tập liên quan đến bội số trong bài viết dưới đây nhé!
Contents
- 1 Khái niệm bội số là gì? Ước số là gì?
- 2 Bội số chung là gì?
- 3 Bội số chung nhỏ nhất (BCNN)
- 4 Cách tìm bội số chung nhỏ nhất – Công thức tổng quát tính BCNN
- 5 Các dạng bài tập về bội số chung nhỏ nhất
- 6 Dạng 3: Dạng bài toán đưa về việc tìm bội chung thỏa mãn điều kiện cho trước của hai hay nhiều số.
- 7 Bài tập vận dụng tìm bội chung.
- 8 Lời Kết
Khái niệm bội số là gì? Ước số là gì?
Bội số và ước số là một trong số những khái niệm xuất hiện trong chương trình Đại số mà nhiều bạn học sinh lớp 6 rất dễ nhầm lẫn khi mới học bởi khi đó chưa thực sự hiểu rõ về 2 khái niệm này. Bội số, ước số được định nghĩa tổng quát như sau:
- Bội số của A là tập hợp gồm những số chia hết được cho số A. Ký hiệu là B (A).
- Ước số là một số tự nhiên thỏa mãn điều kiện có một số tự nhiên khác chia hết được cho số đó. Ước số của A là tập hợp số được kí hiệu là U (A).

Tóm lại: Xét 2 số tự nhiên A và B: Nếu số tự nhiên A chia hết được cho số tự nhiên B thì A được gọi là bội số của số B, đồng thời B lại là ước số của số A.
Bội số chung là gì?
Bội số chung là tập hợp gồm những số nguyên dương thỏa mãn điều kiện chia hết cho từ hai số tự nhiên khác trở lên.
Ví dụ:
- Bội số của 10 là các số 10, 20, 30, 40, 50, 60,… Bội số nhỏ nhất của 10 là 10.
- Bội số của 50 là các số 50, 100, 150, 200, 250,…. Bội số nhỏ nhất của 50 là 50.
- Bội số của 100 là các số 100, 200, 300, 400, 500,… Bội số nhỏ nhất của 100 là 100.
- Bội số của 1000 là các số 1000, 2000, 3000, 4000, 5000,…. Bội số nhỏ nhất của 1000 là 1000.
Một số tính chất của bội chung:
- Nếu A chia hết được cho B và B lại chia hết được cho C thì suy ra A cũng sẽ chia hết cho C. Theo đó: A ⋮ B, B ⋮ C => A ⋮ C. Ví dụ: 8 ⋮ 4 và 4 ⋮ 2 thì 8 ⋮ 2.
- Mọi bội số của A đều chia hết được cho B khi số A chia hết cho số B. Theo đó: A ⋮ B => A.m ⋮ B.
- Nếu A ⋮ C và B ⋮ C thì (A + B) ⋮ C và (A – B) ⋮ C.
Bội số chung nhỏ nhất (BCNN)
Bội số chung nhỏ nhất được hiểu là số nhỏ nhất khác 0 trong tập hợp các số chia hết được cho hai hoặc nhiều số tự nhiên khác nhau. Bội số chung nhỏ nhất được viết tắt là BCNN (a,b).
Sẽ không tồn tại một số nguyên dương nào thỏa mãn chia hết được cho cả A và B nếu A và B đều bằng 0. Bội số chung nhỏ nhất khi đó được quy ước bằng 0.
Ví dụ: Bội số chung của 2 và 3 là tập hợp mà gồm các số tự nhiên chia hết được cho cả số 2 và số 3 đồng thời thỏa mãn điều kiện #0. Theo đó, ta có thể tìm được dễ dàng 6 chính là bội số chung nhỏ nhất của 2 và 3. Bởi số 6 là số tự nhiên khác 0 và là số nhỏ nhất chia hết đồng thời cho cả 2 và 3. Ta có BCNN (2,3) = 6.
Lưu ý: Mọi số tự nhiên đều là bội số của số 1 vì thế với mọi số tự nhiên a và b # 0 ta có:
- BCNN (a,1) = a
- BCNN (a,b,1) = BCNN (a,b).
Cách tìm bội số chung nhỏ nhất – Công thức tổng quát tính BCNN
Để tìm được bội số chung nhỏ nhất một cách nhanh và chính xác bạn có thể tham khảo cách tìm dưới đây để áp dụng tìm ra đáp án đúng nhé!
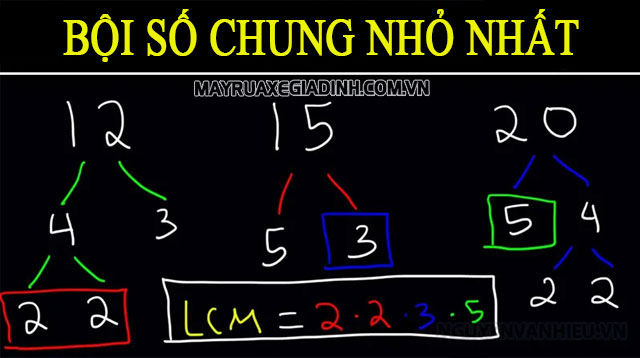
- Bước 1: Phân tích các số đã cho thành các thừa số nguyên tố.
- Bước 2: Từ các thừa số nguyên tố đã phân tích cần chọn ra các thừa số chung, riêng.
- Bước 3: Với các thừa số đã chọn hãy lập tích của chúng, lấy với số mũ lớn nhất của mỗi thừa số. Tích đó chính là bội số chung nhỏ nhất của các số đã cho mà chúng ta cần tìm.

Ví dụ: Tìm BCNN (3, 6, 9)
Trước hết ta cần phân tích các số 3, 6, 9 thành các thừa số nguyên tố. Ta có:
3 = 3
6 = 2.3
9 = 3.3 = 32
Chọn ra các thừa số nguyên tố chung và riêng đó là: 2 và 3. Số mũ lớn nhất của 2 là 1, số mũ lớn nhất của 3 là 2. Do đó:
BCNN (3, 6, 9) = 2. 32 = 18.
Lưu ý:
- Cách tính bội số chung nhỏ nhất của các số mà có từng đôi một số nguyên tố cùng nhau đó là tích các số đó. Ví dụ: BCNN (2, 3, 5) = 2.3.5 = 30.
- Trong các số đã cho nếu xuất hiện một số lớn nhất là bội số của các số còn lại thì số lớn nhất đó chính là bội chung nhỏ nhất cần tìm. Ví dụ: BCNN (2, 3, 6) = 6.
- Nếu b là bội số của a thì bội chung nhỏ nhất của a và b chính là b. Tổng quát: BCNN (a,b) = b (b ⋮ a).
Các dạng bài tập về bội số chung nhỏ nhất
Dạng 1: Tìm bội chung nhỏ nhất của các số đã cho trước.
Phương pháp giải:
Thực hiện cách tìm bội chung nhỏ nhất của các số đã cho đã được nêu ở trên để tìm bội chung nhỏ nhất của chúng. Hoặc bạn có thể nhẩm nhân số lớn nhất lần lượt với 1, 2, 3,…. cho tới khi kết quả là một số mà nó chia hết được cho các số còn lại để tìm bội chung nhỏ nhất của các số đã cho. Tuy nhiên các bạn cần phải nắm chắc được kiến thức về phép tính nhân nếu thực hiện cách tìm bội chung nhỏ nhất theo cách nhân nhẩm này.
Dạng 2: Dạng bài toán về việc tìm BCNN của một hay nhiều số.
Phương pháp giải:
Từ đề bài đã cho cần phân tích đề bài để đưa việc tìm bội chung nhỏ nhất của hai hay nhiều số dựa vào suy luận và kinh nghiệm làm bài.
Ví dụ:
Hai bạn Nam và Minh học cùng một trường nhưng khác lớp. Nam cứ 10 ngày lại trực nhật và Minh thì cứ 12 ngày lại trực nhật. Cả hai đều trực nhật cùng vào một ngày lần đầu. Hỏi hai bạn sau ít nhất bao nhiêu ngày thì lại cùng trực nhật?
Lời giải:
Ta có: Số ngày trực nhật lặp lại của Nam là bội của 10 và số ngày trực nhật lặp lại của Minh là bội của 12.
=> Khoảng thời gian để trực nhật cùng nhau của Nam và Minh chính là bội số chung của 10 và 12.
Vì thế, khoảng thời gian trực nhật cùng nhau từ lần đầu tiên cho đến lần thứ 2 của Nam và Minh là BCNN (10, 12).
Phân tích: 10 = 2.5
12 = 2.2.3 = 22.3
=> BCNN (10,12) = 22.3.5 = 60.
Kết luận: Hai bạn Nam và Minh trực nhật cùng nhau sau ít nhất 60 ngày kể từ lần đầu tiên 2 người trực nhật cùng nhau.
Dạng 3: Dạng bài toán đưa về việc tìm bội chung thỏa mãn điều kiện cho trước của hai hay nhiều số.
Phương pháp giải:
- Bước 1: Phân tích đề bài đã cho để đưa về việc tìm bội chung của hai hay nhiều số cho trước dựa theo suy luận và kinh nghiệm làm bài.
- Bước 2: Tìm bội chung nhỏ nhất của các số đề bài đã cho.
- Bước 3: Từ bội chung nhỏ nhất đã tìm được ở bước 2 cần tìm bội chung.
- Bước 4: Chọn bội nhỏ nhất trong số các bội đó sao cho thỏa mãn điều kiện đã cho.

Bài tập vận dụng tìm bội chung.
Ví dụ: Tìm bội chung nhỏ nhất và Bội chung của:
- 20 và 52
- 22, 30 và 50
- 3, 9, 13
- 42, 70, 180
Lời giải:
a, 20 và 52
Ta có: 20 = 2.2. 5= 22.5
52 = 22.13
=> BCNN (20, 50) = 22.5.13 = 260
=> BC (20, 52) = 260k (k ∈ N*) hoặc BC (20, 52) = {260, 520, 780, 1040,…}
b, 22 và 30
Ta có: 11= 11
22 = 2.11
30 = 2.3.5
=> BCNN (11, 22, 30) = 2.3.5.11= 330
=> BC (11, 22, 30) = 330k (k ∈ N*) hoặc BC (11, 22, 30) = {330, 660, 990, 1320, 1650,…}
c, 9 và 13
Ta có: 3 = 3
9 = 32
13 = 13
=> BCNN (3, 9, 13) = 32.13 = 117
=> BC (3, 9, 13) = 117k (k ∈ N*) hoặc BC (3, 9, 13) = {117, 234, 351, 468, 585,….}
d, 42, 70, 180
Ta có: 42 = 2.3.7
70 = 2.5.7
180 = 2.90 = 22.32.5
=> BCNN (42, 70, 180) = 22.32.5.7 = 1260
=> BC (42, 70, 180) = 1260k (k ∈ N*) hoặc BC (42, 70, 180) = {1260, 2520, 3780, 5040,….}
Lời Kết
Như vậy chúng ta đã vừa tìm hiểu chi tiết về bội số là gì cũng như cách tìm bội số chung nhỏ nhất. Hy vọng, bài viết này hữu ích giúp các bạn hiểu bội số là gì và qua đó có thể áp dụng để giải nhanh, chính xác các bài toán liên quan đến phần kiến thức này.